技术的真相 I 智慧物流创新业务场景下的运筹优化实践综述
Differences may exist in the goals to be achieved, the particular processes involved, and the magnitude of effort. Nevertheless, it is possible to abstract the underlying essential similarities in the management of these seemingly disparate systems.
George Dantzig
Linear Programming and Extensions,1963

编者按
在《技术的真相 I 原来618物流这么快的背后是求解数学题》这期中,我们介绍了智慧物流场景中仓内智能机器人任务的分发及执行的相关内容。但是,关于人工智能如何赋能到物流的各个环节,帮助企业降本增效的问题,其实是需要拆解成很多场景,很多技术去探讨的,本篇内容,我们就带大家一起走入另一个“真相”中。
在管理科学领域,运筹学的研究和发表存在明显的鄙视链,即数学>理论运筹>计算运筹>应用运筹,乃至管理科学的期刊中甚至一些应用学科的顶刊也只能跻身Tier 2&3。
但经过多年的物流和供应链的跨领域实践,我们意识到,这两者不仅不是割裂的,甚至是相互促进的,社会经济的方方面面为优化理论的应用提供了广阔的场景,应用场景的拓宽带动计算工具的发展,也为理论运筹贡献了更多的课题。
我们将从智慧物流的业务场景入手,对一些业务场景通过数学模型进行新的诠释。这篇文章尽量通过通俗的、非数学的语言介绍我们在优化实践中的一些思考,我们将指出这些非技术的思考对于算法的实现和成功落地是大有裨益的。
一、简述
运筹学是包含数学等多种学科的综合性学科,其使用科学的方法、技术和工具对生产、管理等事件中出现的一系列带有普遍性的最优决策问题加以提炼,然后使用数学方法进行解决,以便为管理人员提供问题最佳的解决办法,一般地需要包含“寻找在满足约束的条件下能够最大化/最小化某一目标的最优决策”这一过程。
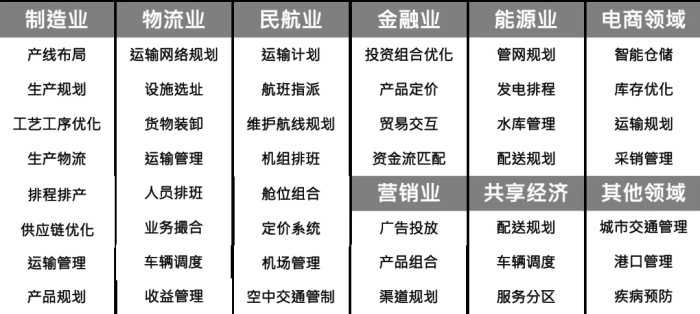
以上定义天然带有问题导向、应用为先的倾向,也因此,很多专业都涉及应用运筹且工业运筹团队往往需要来自不同专业中的学者和专业人员,如数学、工业工程、交通科学、机械自动化、电子和计算机以及管理科学等,团队中的专业组成往往决定了领域知识(Domain Knowledge)的倾向性以及技术选择。
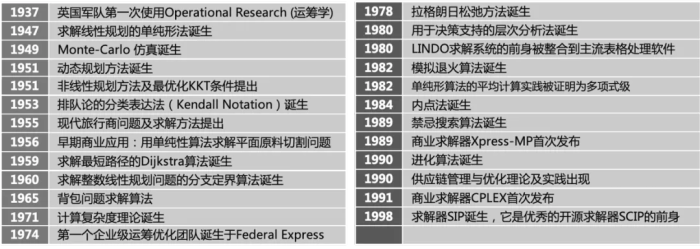
现代运筹学经历了80多年的发展,和几乎所有技术一样,是应用、理论交替发展的。比如早期的军事应用和计算机的运用促进了计算运筹学的出现,而最早的cutting stock问题则在列生成方法诞生前就提供了这一方法的直观运用。如果我们非要对现代运筹学的发展进行阶段的划分,那么可以有如下几个阶段。
1. 40年代。现代运筹学起源于第二次世界大战期间,盟军迫切需要受用数学模型解决各种作战问题,将有限的人力和物资分配和投放到各种军事活动当中以达到最好的作战效果。如英军使用数学模型优化对德雷达分布、反潜力量分布、规划战略轰炸路线等。这些问题的解决确保了最后的胜利,也开创了现代运筹学军事应用的先河。
2. 50-80年代。二战结束后,学者们将战争中取得的运筹学研究成果广泛地应用到政府管理以及生产、服务和金融行业中,随着应用范围的扩大,运筹学各重要分支也得到快速发展,大量理论模型和算法涌现,计算机的出现也使得算法的应用可以更快速和标准化,如单纯形法诞生5年后,美国空军就在第二台UNIVAC I型电脑上实现了该算法程序。
3. 90年代。计算机技术的快速发展伴随着计算力的提升和商业求解器的出现,人们可以解决的问题规模和复杂程度不断提升,这催生了更多的研究需求,各种优化算法及其变种的实现相继出现,早期的商业求解软件也开始面向市场。
4. 2000年后。一方面,经济活动的日益发展让运筹优化理论焕发新的生机,既有的理论可以应用到全球整合供应链优化、电商场景下的仓配优化以及生产环节的柔性和智能制造等新经济环节,人工智能、机器学习及仿真技术也开始和运筹优化开始交叉,产生了一系列新的学术成果。
应用运筹目前在各个领域均有渗透,并支撑了行业的业务创新、降本增效和规模扩张,目前在国际上已经设立了多项工业运筹和运筹实践奖项,以表彰商业和非商业组织在运筹实践上的卓越成果,比较著名的包括Informs Prize和Franz Edelman Award。其中,Informs 奖旨在表彰将运筹优化有效整合到机构决策过程中的公司,1991年至今获奖企业包括联邦速递、美航、联航、辉瑞制药和福特等。遗憾的是,尚未有一家中国公司能够进入奖项的最终名单。
最早在决策过程中引入优化理论的民用行业是汽车制造和航空,在此我们简要介绍2个案例。
01
通用汽车的产线提效和安吉星(OnStar)战略决策(2005年Franz Edelman Award)
20世纪80年代末,通用汽车生产效率远低于竞争对手,91年的亏损达到45亿美元,通用汽车的研发部门开启了长期的产线吞吐量提升项目Test Improvement Process。吞吐量提升可分为建模与算法设计,数据收集以及全流程优化三个子问题,经过20年的努力,TIP广泛应用到通用全球工厂,极大的提高了生产效率,带来了21亿美元收益。1997年,通用汽车研发的OnStar系统即将进入市场,由于市场未知,通用决定使用运筹学方法进行OnStar市场策略战略决策;通用建立了多方法模型,结合动态规划及仿真分析等对所有可能的市场策略进行评估与决策。OnStar系统的战略决策使之迅速占领了市场,并给通用带来了近10亿美元利润及长久的竞争优势。
02
美航的收益管理和人员排班优化(1991年Franz Edelman Award)
人员排班每年给AA带来超过13亿美元的成本,结合运筹优化手段(集合分割问题/拉格朗日松弛/混合算法),美航推出了航程重评估改善系统TRIP,极大提高了人员排班效率,将原有的人员利用率提高了1.5%。TRIP系统每年可为美航节约超过2000万美元的成本,并成功外销到其他航空公司和铁路公司。收益管理通常指给定航班及票价后,如何通过对机票预订的动态管控最大化航空公司收益。收益管理是复杂的动态决策问题,可拆分为机票超卖,折扣分配及转机管理三个规模较小、可以求解的问题; 通过对上述运筹优化问题的研究,美联推出了DINAMO收益管理系统,该研究三年内(1988-1991)为美联带来了14亿美元的收益。
二、以问题为导向的实践
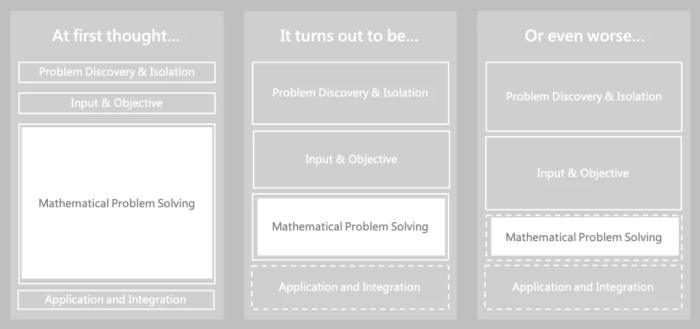
既然应用运筹是寻找在满足约束的条件下能够最大化/最小化某一目标的最优决策,是否意味着在进行运筹优化实践时就好像小学生做应用题一样?其实不然,这一过程一般包括以下7个步骤。
第一步是问题发现、抽象和确定边界。这往往不是个核心技术问题,但是除非业务团队明确的知道问题是什么、问题的解决需要怎样的技术,往往需要技术团队来进行。在应用实践中,问正确的问题往往比解决问题更为重要。
第二步解决数据和目标的问题。和基于训练的学习过程不同,数学模型有着明确的、基于业务和实际KPI的目标,然而目标往往是多样的,跨部门合作会进一步带来目标上的利益冲突,平衡这种冲突同样不太是一个核心技术问题,但的确决定了一个运筹优化实践项目是不是一开始就注定以失败告终。另一方面,尽管优化建模不是data-driven的,不需要大量数据用于模型训练,但是数据的质量决定了模型的复杂度,比如是否需要为数据的不确定性引入更复杂的非线性约束。
第三步是模型的数学表达。这一步即将问题表达成目标+约束的数学形式。所谓数学模型的建立一般就是指这一步。建模有很多具体的技巧,包括变量的选择、增加维度降低模型求解难度、多目标的处理、条件约束的线性化、非线性约束的线性化、解空间的预先修剪等等。尽管一些数学模型是难以在合理时间内求得精确解的,建立数学模型仍然是必要的一步,它将模糊的业务语言转化为了精确的数学语言,是放之四海而皆准的通用化表达。这一步确立了应用题的题干。
第四步是问题的求解。如前所属,出于种种原因可能我们无法利用求解器求得精确解,这时转而寻求启发式或元启发式方法是更为实际的。对于最优解没有强需求的问题,或者对于求解时间有限制的场景,求得满足要求的可行解需要能够对于解的质量有很好的评估。
第五步是对解的解读。通常涉及将数学模型的解转化为业务语言上的决策和建议。有些时候,这种解读是直观的;也有可能是复杂的,如需要结合最优解下约束的松紧与否给予业务上的对应含义。
第六步是模型求解的迭代。这种迭代的需求有两个来源,一是业务不断明确问题边界、约束和目标更新带来的;二是求解过程对于解的质量、时间和资源消耗的约束带来的。我们经常遇到业务一开始对于目标、约束和可决策变量莫衷一是模棱两可,但是看到解之后认为不符合直觉和运营实际,需要修改问题定义的情形,按照瀑布的开发方式来说这算需求的变更,然而这却是必然会出现的过程,你不可能要求业务去精确描述一个模糊存在的流程和惯例中需要被纳入模型考量的要素。对于模型边界通过求解迭代过程不断完善是一个应用运筹项目成功的必要因素。
第七步是算法的应用并被集成到系统中。
从算法团队自身角度出发,一开始觉得数学的运用是关键(三至六步),是需要我们花费最多精力雕琢的,其他的都是输入输出,是自然而然的被定义好的。而如上图所示,大量的工作在问题的发现和定义上,是否能够应用除了技术上的考虑,还要考虑实现的方便与否、求解时间能否接受、业务约束能否确定边界、使用人员能力高低等等;更有甚者,很多问题甚至在问题定义阶段就确保了后面无法落地实施。如果我们陷入技术先进性的迷思,就可能导致算法团队建模能力很强但没有实际产出。为此,以解决问题为导向的运筹优化实践是必要的。
三、解决应用运筹若干挑战
成功的运筹优化应用需要有定义明确的需求和问题、恰当的理论支撑、先进的工具支持和可落地的应用方式。这些要素也构成了几方面的挑战。
(一)寻找需求
上图是米开朗基罗创作的「创造亚当」,画中上帝伸手接触亚当给予启迪。然而我们的问题是在工业界的运筹实践中,谁才是亚当?
当业务方已经意识到了问题,并且可以把问题界定出来,甚至知道可以使用运筹优化方法(而不是别的什么方法)解决问题。算法就是亚当,双方如知己一般,一拍即和,需求可以被快速响应。然而问题是,在我们接触到的国内客户中,大部分知道需求不知道方法,甚至连问题都没有很好的认识。
如果反过来呢,算法团队需要去理解客户的问题和痛点、从自身能力给出场景-问题-方法的三元组,在协助客户明确需求后,再去做算法该做的事。一方面,这要求算法团队具备咨询、售前方案、POC验证和一定的销售能力,另一方面这种需求获取的成本高、时间长,且需要对客户进行教育,对于技术能力低的客户往往无法奏效。
哪种方式在国内都不是特别的合理,对于这个问题我们只能说要按照客户的水平进行判断,双方各进一步。而对于客户的选择倾向又是一个离题太远的非技术课题了。
(二)恰当的理论支撑
所谓恰当的理论支撑正是指选取适于问题、便于求解、可实现的方法论。现代运筹学80年的理论发展为实际业务场景的应用形成了有利支撑。但目前学科方向已经高度分化,理论运筹学、计算运筹学以及和各个专业交叉产生的应用运筹学各自有学术圈子。考虑到运筹团队有较强的学术背景,成员的学术背景实际上决定了算法团队的工作模式。太多理论背景的人倾向于不(屑)考虑实际应用,做应用场景的有各自的领域,不容易跳出来思考问题。团队要形成全面的理论和应用各取所长,不断进取的风气。
(三)先进的工具支持
运筹优化问题的求解需要使用求解器。
在这一点上,首先我们要认清,没有必要的环境不要尝试重复开发轮子。很多人认为求解线性规划不就是使用单纯形法吗,我都可以手撸一个线性求解器。这就好像很多人认为系统仿真不就是按照时间处理事件么,我可以手撸一个仿真系统。如果事情真的这么简单,为什么没有一款国产通用求解器和通用多范式仿真平台能够拿的出来呢?
事实上,用任何语言复现单纯形算法都是一个本科相关专业学生可以做到的事情,但是真正可以做到通用求解器的规模要做的更多,比如如何做出一门偏向自然语言的建模语言、如果进行问题的预处理、如何通过反复的对偶单纯性加速线性求解的性能、使用何种框架解决整数规划问题、如何让框架支持多款线性求解器、如何使分支定界策略支持自定义的启发式搜索和自定义的求解过程、如何并行搜索、如何配置各种启发式搜索的参数以减少用户定制求解过程的必要、如何根据问题结构进行自动化的求解过程选择和参数配置、如何使得框架能够解决二次和非线性的规划、如何解决非数集合上的约束规划问题、如何整合求解器对于其他求解引擎和语言的支持、如何使框架支持问题分解策略、如何自定义问题分解、如何进行热启动等等。
好的求解器不光是技术上的先进,其工程上的也做了大量的优化工作,而这些没有时间上的积累是不可能的。即使是目前国内最响亮的杉数COPT求解器也仅仅是实现了线性这部分,涉及复杂整数问题仍需要定制求解过程来进行,杉数背靠了上财可以有进行廉价的高技术开发,尚且如此。
为此,如果场景要求我们寻求问题的精确解,我们需要选择一款合适的求解器。这时,我们就会面临到求解器不可能三角。
在服务中集成商业求解器或求解环境是极为昂贵的,比如供应链优化软件LLamaSoft旗下的SCGX供应链优化大师就继承了Xpress的OEM版本,但是SCGX的本身单个许可证售价达到了70万人民币/年。
可想而知,我们基本上可以放弃在业务中使用商业求解器的念头。而对于开源求解器来说,又往往遇到性能问题。我们在该专题的后续文章中,会持续的推广使用目前最先进的SCIP开源求解器,其综合性能相对三大商业求解器来讲已经可以望其项背。
(四)算法实现上的妥协
我们给出几个实际的例子来说明。
1. 算法与开发。运筹算法团队的人员对于系统开发不甚了解,同样开发人员对于运筹算法的实现和机理也不了解。两者合一固然最好,但往往不可得。解决这问题的最好方式就是算法团队必须提供可交付的算法,这对算法团队提出了更高的要求。
2. 时效要求。运筹算法团队在既往的学校研究中往往只做离线的算法研究,也不考虑算法在系统中得性能和实际运行时对时效的要求。如果算法不能针对系统的时效性做调整或妥协,那么即使算法理论上和求解上可圈可点,依然是花瓶,无法实用化。
3. 静态和动态问题求解。很多on-line算法需求场景求解的是一个动态系统的优化问题。对于动态系统进行时间上的离散或者直接求解动态场景不仅是一个算法问题,也是系统和业务场景需要解决的。无法在该问题上达成共识或妥协也会让算法无法交付。
4. 调参和优化。对于复杂的业务场景,运筹优化算法也需要大量的参数来刻画由于人为偏好、误差、时间、业务逻辑变更等原因带来的目标、约束和参数改变。为此也需要进行参数调优,这是理论模型常常一笔带过的。
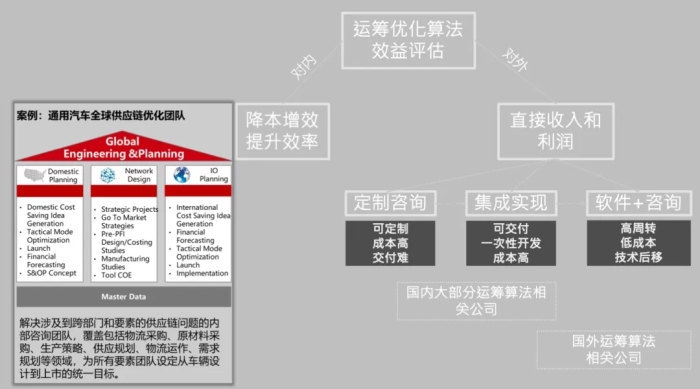
(五)算法落地方式和效益评估
以问题为导向的运筹优化实践最终要求解决问题,也就是落地。解决问题的方式却不止一种,我们按照需求是内生还是外生的来区分。
对内来说,算法的效益通过达成的降本增效来体现。例如通用汽车全球供应链优化团队Octupus负责车型从SOP到停产过程所涉及到的全球供应链协作过程中存在的所有优化问题,直接对接需求并进行跨组织业务目标的优化,较高的授权级别使得这种Internal Consulting部门在面对问题时可以不拘泥一某个组织的目标和利益。
对外来说,算法的效率则与直接收入挂钩,这即是将算法作为一种服务和产品来进行销售。根据经验会有定制咨询、集成开发、软件+咨询这三个阶段。
1. 在第一个阶段,算法以模型和文档提供咨询服务,这对于客户的要求很高,即能为咨询服务支付费用并仅依靠所交付的文档和模型来实现算法价值。如果客户对问题没有清楚的认识、无法为知识支付咨询费用、没有技术实力将咨询成果转化并产生效果,那么这种方式是困难的。
2. 第二个阶段是将模型按照软件或者系统的方式集成到客户的系统和业务流程中去,这种集成是定制化的,客户需要支付一次性开发费用,通常会带来高昂的成本。但另一方面,对客户转化知识的能力要求降低了,客户只需要有必要的关键用户可以使用该软件和系统即可。这种模式中,运筹优化算法是重要的增值项。
3. 对于一部分场景来说,重复进行定制开发是不经济的,它要求算法团队长期处在相对前端的位置从而增加项目成本且定制化成本无法被分摊。更好的方式即是通过标准化产品实现产品成本均摊、通过可配置化实现低成本快速的定制化交付,算法技术团队可以后移,而前端交给解决方案和咨询顾问。
对比国内外以运筹优化作为核心产品技术方向的公司的比较分析发现,诸如LLamaSoft, FuturMaster, AIMMS, Hermes等国外公司已经长期处在第三个阶段,而国内的杉数、优桦林和国科优化等公司还仍然处在从第一阶段到第二阶段迈进的阶段。
四、尾声
这篇内容我们尽量使用了通俗的语言进行了介绍,侧重非技术的思考。如果读者有希望探讨或研究的问题,可发邮件至河图算法部(demos@megvii.com),我们将以大家提出的具体问题来进行更偏向技术的探讨,同时要强调这种技术的探讨是以解决问题为导向的技术实践。